بررسی میدانی فیبر نوری

تحقیق در مورد بررسی میدانی فیبر نوری حسینی پویا با فرمت ورد در 27 صفحه تهیه شده است.

فصل1. موجبرهای دی الکتریک
1-1 مقدمه
در این فصل به بررسی موجبرهای دی الکتریک از دیدگاه امواج الکترومغناطیسی خواهیم پرداخت، ابتدا برای ورود به بحث از تحلیل موج در ساختار لوحه دی الکتریک و در ادامه به تار نوری خواهیم پرداخت. کلیه این مباحث مبتنی بر حل معادلات ماکسول در این محیط ها در جهت یافتن عبارات مربوط به میدان های الکتریکی و مغناطیسی امواج انتشاری است.

1-2 موجبر لوحه ای دی الکتریک
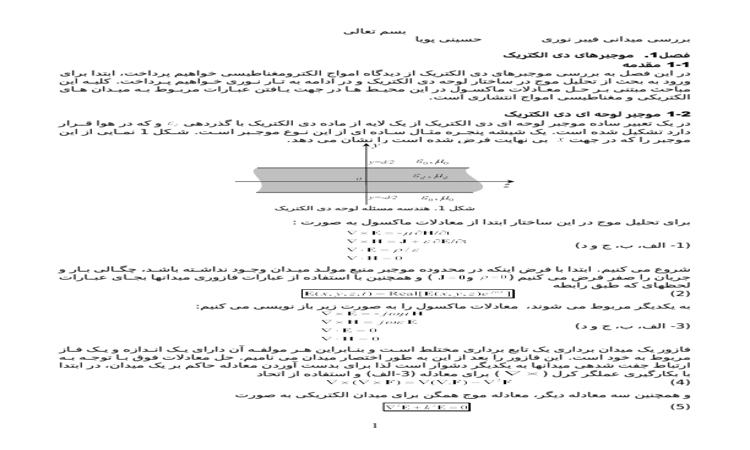
در یک تعبیر ساده موجبر لوحه ای دی الکتریک از یک لایه از ماده دی الکتریک با گذردهی و که در هوا قرار دارد تشکیل شده است. یک شیشه پنجره مثال ساده ای از این نوع موجبر است. شکل 1 نمایی از این موجبر را که در جهت بی نهایت فرض شده است را نشان می دهد.

شکل 1. هندسه مسئله لوحه دی الکتریک

برای تحلیل موج در این ساختار ابتدا از معادلات ماکسول به صورت :
(1- الف، ب، ج و د)
شروع می کنیم. ابتدا با فرض اینکه در محدوده موجبر منبع مولد میدان وجود نداشته باشد، چگالی بار و جریان را صفر فرض می کنیم ( و ) و همچنین با استفاده از عبارات فازوری میدان­ها بجای عبارات لحظه­ای که طبق رابطه
(2)
به یکدیگر مربوط می شوند، معادلات ماکسول را به صورت زیر باز نویسی می کنیم:
(3- الف، ب، ج و د)
فازور یک میدان برداری یک تابع برداری مختلط است و بنابراین هر مولفه آن دارای یک اندازه و یک فاز مربوط به خود است. این فازور را بعد از این به طور اختصار میدان می نامیم. حل معادلات فوق با توجه به ارتباط جفت شده­ی میدانها به یکدیگر دشوار است لذا برای بدست آوردن معادله حاکم بر یک میدان، در ابتدا با بکارگیری عملگر کرل () برای معادله (3-الف) و استفاده از اتحاد
(4)
و همچنین سه معادله دیگر، معادله موج همگن برای میدان الکتریکی به صورت
(5)
در مورد میدان مغناطیسی نیز با باتکرار روش فوق البته با شروع از معادله دوم به رابطه مشابه
(6)
این معادلات را معادلات برداری موج همگن یا معادلات موج برداری هلم هولتز می گویند. عدد موج در معادلات فوق شامل اطلاعاتی مربوط به فرکانس موج و مشخصات محیط می­باشد. با توجه به اینکه در مسئله لوحه شکل1 با دو محیط روبرو هستیم، بنابراین اعداد موج محیط­ها به صورت

(7) و
به ترتیب برای داخل لوحه و برای خارج لوحه، می باشند. این معادلات با در نظر گرفتن شرایط مرزی مانند هر معادله دیفرانسیلی قابل حل هستند. در اینجا ما با انتخاب دستگاه کارتزین و با فرض اینکه موج در جهت و با ثابت فاز در داخل و خارج لوحه بدون اتلاف () منتشر شود میدان را به صورت

(8)
در نظر می گیریم (در حالت کلی تر می توان به جای از ثابت انتشار استفاده کرد). این فرض، همانطور که استفاده از فازورها باعث حذف متغیر زمان و مشتقات آن شد ()، در اینجا باعث حذف متغیر و مشتقات آن خواهد شد (). بالانویس صفر به معنی در است. با این مفروضات معادلات هلم هولتز به صورت زیر در می آیند:
(9- الف و ب)
ضریب را مقدار ویژه معادله می نامیم. توان دوم این مقدار ما را گول نزند، اگر این مقدار ویژه مثبت باشد () جواب های معادله فوق بصورت ترکیب خطی توابع سینوسی و کسینوسی و در غیراینصورت () به صورت ترکیب خطی توابع نمایی افزاینده و کاهنده خواهد بود.
بیایید به مسئله خودمان یعنی شکل 1 برگردیم. در اینجا هندسه بگونه ای انتخاب شده است که میدانها به خاطر یکنواختی لوحه در جهت از این متغیر مستقل هستند به عبارت دیگر اگر مقدار میدان برای یک نقطه معین مورد نظر باشد کافیست مقدار عرض نقطه را بدانیم و طول آن در مقدار میدان اهمیتی ندارد. بنابراین در مورد میدان عرض می توان گفت: و رابطه (9) نیز به صورت ساده تر :

(10- الف و ب)
ظاهر می شود. فراموش نکنید بردار دارای سه مولفه و است. بنابراین هر معادله دیفرانسیلیِ برداریِ فوق در واقع شامل سه معادله دیفرانسیل عددی است، می­دانیم که معادلاتِ کرلِ ماکسول ( و )، بین مولفه های مختلف ارتباط برقرار می کنند؛ با توجه به این اکنون این سوال مطرح می­شود که آیا نیاز به حل همه شش معادله عددی (10) هست و اگر نیست معادله دفرانسیل مربوط به کدام مولفه را ترجیح می­دهیم ابتدا حل کنید؟
برای روشن شدن پاسخ این سوال ابتدا معادلاتِ برداریِ کرل را با فرض انتشار موج در جهت همانطور که در (8) بیان شد، برای مولفه های سه گانه آن به صورت معادلات عددی زیر

(11- الف، ب و ج)
(12- الف، ب و ج)
بیان می نماییم. معادلات (11-الف) و (12-ب) را درکنار هم به صورت یک دستگاه شامل دو معادله و دو مجهول در نظر بگیرید. معلوم را بگیرید و به طرف راست و مجهول ها را و فرض نموده و به طرف چپ منتقل کنید. اکنون با حل دستگاه
(13)
و به طور مشابه با کنارهم قراردادن (11-ب) و (12- الف) و تشکیل دستگاهی دیگر برای بقیه، ، ، و را به صورت
(14)
بدست می آیند. چون میدان ها تابعی از نیستند؛ مشتقات جزئی نسبت به را می­توان با صفر جایگزین کرد اما برای کلی بودن روابط آنها را فعلاً نگهداشته ایم.
آیا سوالی که قبلاً مطرح شده بود را هنوز به یاد دارید؟ آری، این روابط به روشنی بیان می­کنند که با معلوم بودن مولفه های جهت ( و )، به سادگی عبارات سایر مولفه ها را در اختیارمان قرار می گیرد. بدین سبب حل (10- الف و ب) به حل دو معادله دیفرانسیل

(15- الف و ب)
مختصر می شود. اکنون سوال دیگری را مطرح می کنیم؛ آیا و به هم وابسته هستند؟ یعنی می توان یکی را بذحسب دیگری محاسبه نمود؟ جواب منفی است این دو مولفه مستقل هستند(چرا؟). این امر تحلیل را ساده تر می کند زیر می توان اثر حضور هر یک را به طور جداگانه بررسی نمود.

1-2-1 مود TM در لوحه دی الکتریک
حالتی را در نظر بگیرید که میدان مغناطیسی مولفه ای در جهت انتشار نداشته با شد (). بنابراین تنها معادله دیفرانسیلی که باید حل شود معادله (15-الف) است. اکنون برای اینکه موجی در این لوحه محصور باشد بایستی مقدار را مدیریت کنیم تا معادله در داخل و خارج لوحه دارای جواب دلخواه (موج محصور شده) باشد.
خارج لوحه ( و ) : برای خارج بهترین جواب اینست که میدان ها صفر باشد اما این بدین معنی است که ناحیه خارج بجای هوا (دی الکتریک)، هادی کامل باشد؛ که هندسه مسئله اینگونه نیست. لذا از بین توابع سینوسی و توابع نمایی، شکل نمایی کاهنده را با ضریب میرایی را انتخاب می کنیم. این فرض زمانی حاصل خواهد شد که انتخاب شود.
داخل لوحه (): برای داخل لوحه گزینه توابع سینوسی (فرد) یا کسینوسی (زوج) وجود دارد. از آنجا که توابع سینوس و کسینوس نیز به هم وابستگی ندارند بنابراین تفکیک مود TM به زوج و فرد نیز کار را ساده می نماید. این توابع نیز با انتخاب ، که ثابت فازاست، پاسخ معادله (15-الف) خواهند بود.

1-2-1-الف TM فرد
شکل 2 معادلات مختلف در هر ناحیه را برای موج TM فرد نشان می دهد. مولفه میدان الکتریکی عرضی در داخل به صورت
(16)
و در خارج به صورت
(17) و
(18)
می باشد. همانطور که در این شکل مشاهده می شود منحنی تغییرات مولفه میدان الکتریکی تابعی فرد است که از بخشی از شکل تابع سینوسی در داخل و دو تابع نمایی کاهنده در بیرون تشکیل شده است.

شکل 2 مود TM فرد در لوحه دی الکتریک

در این شکل ما منحنی را در داخل و خارج لوحه پیوسته کشیده ایم؛ آیا حقیقتاً چنین است؟ آری، برمبنای شرایط مرزی الکترومغناطیسی در محیط بی اتلاف، بایستی مولفه مماسی میدان الکتریکی و مغناطیسی در مرز دو محیط پیوسته باشند و در اینجا مولفه های در جهت و مماسی هستند. لذا مقدار دامنه های مولفه میدان الکتربکی در بیرون، بر حسب دامنه میدان داخلی، به صورت زیر قابل محاسبه هستند:

(19)

(20)
با قراردادن این مقادیر در روابط (17) و (18) مولفه میدان الکتریکی عرضی در خارج به صورت
(21)
(22)
در می­آیند. سه عبارت (16) ، (21) و (22) و سه مولفه ی میدان مغناطیسی، که صفر هستند، را در رابطه (14) قرار داده و سایر مولفه ها به ترتیب برای بالا، درون و پایین لوحه به صورت زیر بدست می آیند.

(23)
(24)
(25)
و شکل لحظه ای میدان های موج را با در نظر گرفتن روابط (2) و (8) و روابط بالا، در جدول زیر آمده است.

جدول 1 مشخصات موج در ناحیه بالای لوحه () مود TM فرد
میدان الکتریکی

میدان مغناطیسی

جدول 2 مشخصات موج در ناحیه داخل لوحه () درمود TM فرد
میدان الکتریکی

میدان مغناطیسی

جدول 3 مشخصات موج در ناحیه پایین لوحه () درمود TM فرد
میدان الکتریکی

میدان مغناطیسی

جداول 1 و 3 نشان دهنده توزیع فرد میدان در خارج هستند ().
اکنون این سوال مطرح می شود که مقادیر ، و چگونه بایستی تعیین شوند؟ مقدار ویژه در هر ناحیه را به یاد بیاورید که به صورت
(26)
تعریف شد. با تفاضل این دو رابطه، به صورت
(27)
حاصل می آید. از آنجا که مقادیر و هردو حقیقی و مثبت هستند بنابراین رابطه فوق مبین بخشی از دایره است که در یک چهارم اول قراردارد. شعاع این دایره به صورت
(28)
است و مقدار آن با فرکانس موج رابطه مستقیم و خطی دارد.
به یاد دارید که از دو شرط مرزی بیان شده فقط یکی را استفاده کردیم و رابطه دامنه ها را یافتیم؛ شرط مرزی دوم را که مربوط به پیوستگی مولفه مماسی میدان مغناطیسی است و به صورت

(29) مود فرد TM
نتیجه می دهد. منحنی اخیر شبیه منحنی تغییرات تابع تانژانت است. صفرهای آن در
(30)
و مجانب های آن در
(31)
قرار دارند. که n شماره مود TM فرد است. شکل 3 منحنی های مربوط به رابطه (27) و (29) را وقتی امکان انتشار موج در دو مود TM فرد وجود داشته باشد، نشان می دهد.

شکل 3 منحنی های ضریب میرایی، ، برای یافتن مودهای TM فرد
شکل 3 نشان می­دهد که با افزایش فرکانس، مقدار افزایش یافته و اگر شرط
(32)
برقرار شود، تعداد مودهای فرد TM برابر n+1 خواهد بود. با بهره گیری از حالت تساوی این شرط، فرکانس­های قطع نیز برای هر مود قابل محاسبه هستند. علاوه براین این شکل نشان می دهد که موج در مود TM0 فرد، در هر فرکانس امکان انتشار را دارد و اگر فرکانس (یا ) به اندازه کافی کوچک انتخاب شود؛ می توان به لوحه دو مودی دست یافت. ازآنجا که در بین هر دو مود فرد یک مود زوج وجود دارد در بخش بعد شرط دو مودی شدن لوحه را خواهیم یافت.
وقتی چند مود امکان انتشار در موجبر را پیدا می کنند، مانند شکل 3، انتشار این مودها به موج اعمال شده در ورودی بر می گردد اگر موج ورودی تنها یک مود را تحریک نماید فقط موج آن مود انتشار می یابد.

1-2-1- ب TM زوج
شکل 4 معادلات مختلف در هر ناحیه را برای موج TM زوج نشان می دهد. مولفه میدان الکتریکی عرضی در داخل به صورت
(33)
و در خارج به صورت
(34) و
(35)
می باشد. همانطور که در این شکل مشاهده می شود منحنی تغییرات مولفه میدان الکتریکی تابعی زوج است که از بخشی از شکل تابع کسینوسی در داخل و دو تابع نمایی کاهنده در بیرون تشکیل شده است.

شکل 4 مود TM زوج در لوحه دی الکتریک

مقدار دامنه های مولفه میدان الکتربکی در بیرون، بر حسب دامنه میدان داخلی، به صورت زیر قابل محاسبه هستند:

(36)

(37)
با قراردادن این مقادیر در روابط (17) و (18) مولفه میدان الکتریکی عرضی در خارج به صورت
(38)
(39)
در می­آیند. سه عبارت (33) ، (38) و (39) و سه مولفه ی میدان مغناطیسی، که صفر هستند، را در رابطه (14) قرار داده و سایر مولفه ها مشابه مود فرد TM بدست می آیند. شرط مرزی مربوط به پیوستگی مولفه مماسی میدان مغناطیسی نیز به صورت

(40) مود زوج TM
نتیجه می دهد. این منحنی بجز در شبیه منحنی تغییرات تابع کتانژانت است. صفرهای آن در
(41)
و مجانب های آن در
(41)
قرار دارند. که n